blog-web/source/_posts/算法/洗牌算法.md

title	date	tags	categories
洗牌算法	2019-7-22 15:17:24	算法	算法

洗牌算法也就是去随机打乱一个序列的算法 但是是否是真的随机乱序，仍然需要对算法进行验证

准备工作

既然是随机乱序，自然涉及一些生成随机数和交换数组元素的方法 所以可以先写几个工具函数，这个很简单，基本没什么难度

/**
 * 交换数组的两个元素
 * @param {Array<Number>} arr 需要处理的数组
 * @param {Number} index1 第一个元素的索引
 * @param {Number} index2 第二个元素的索引
 */
function swap(arr, index1, index2) {
  let tmp = arr[index1]
  arr[index1] = arr[index2]
  arr[index2] = tmp
}
/**
 * 生成从min(包含)到max(包含)范围内的随机整数
 * @param {Number} min 范围的最小值
 * @param {Number} max 范围的最大值
 */
function randInt(min, max) {
  return Math.floor(Math.random() * (max - min + 1)) + min
}
/**
 * 创建从1到len的序列
 * @param {Number} len 序列长度
 */
function createSequence(len) {
  let result = []
  for(let i=1 ; i<=len ; i++) {
    result.push(i)
  }
  return result
}

洗牌算法

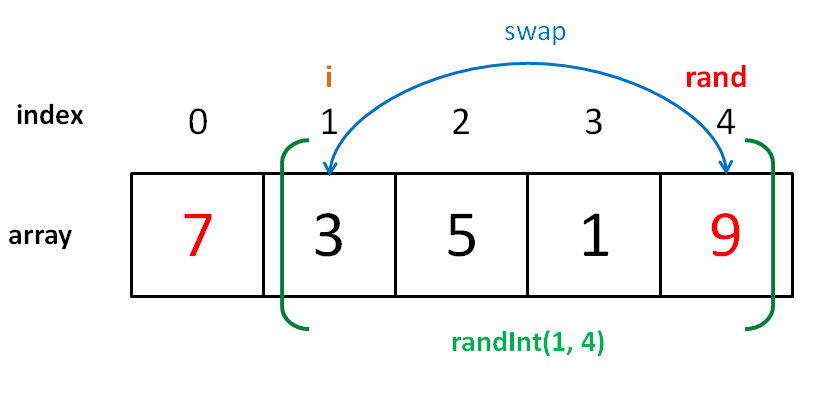
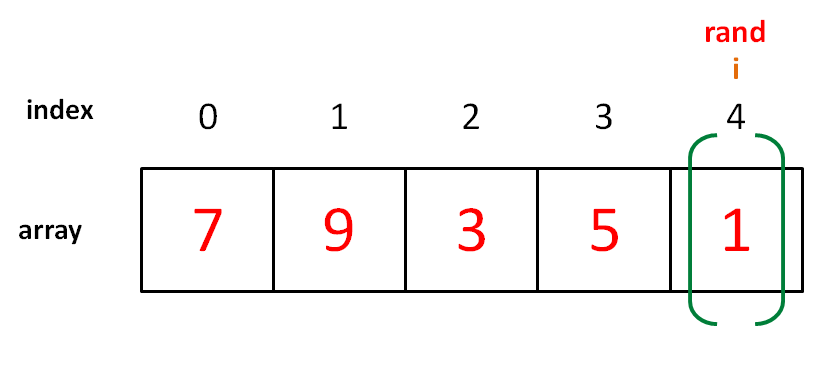
主体的思路是遍历数组，从当前游标之后的元素当中随机选择一个元素与当前游标指向的元素交换

function shuffle(arr) {
  for(let i=0 ; i<arr.length ; i++) {
    let rand = randInt(i, arr.length-1)
    swap(arr, i, rand)
  }
}

需要注意的是每次随机数取值的范围都是包含当前元素的 比如上图中如果随机到的数字是0，当然就是相当于不做交换 此时的随机范围是5，也就是有5种可能的情况，之后每次范围缩小 可能的情况就会-1 总共的情况就是5×4×3×2×1

最后随机范围只剩1个元素，也就只有1种情况

算法验证

有随机范围就有若干种可能性 但是可能性的总数必定是n!，因为对于n个元素，排列组合的总数就是n!

所以总共的可能性必须要是n!或者它的整数倍(通过不同的可能性产生相同的排列) 否则各种排列方式的可能性就会不同

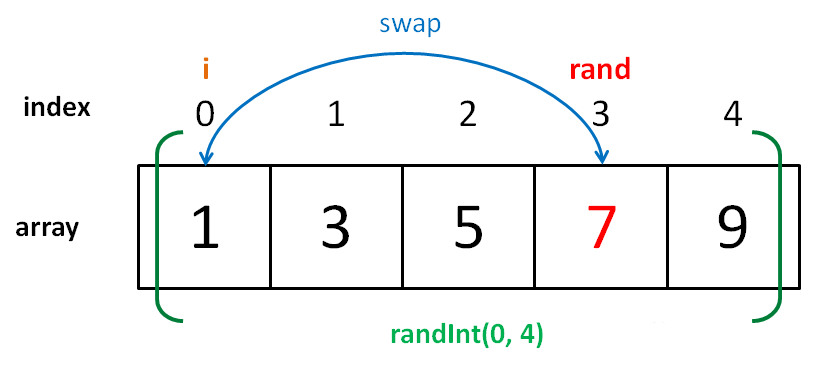
当然这是个必要不充分条件，即使可能的情况有n!，并不代表每种情况出现的概率相同 比如上述的算法实现如果这样写就是错误的

function shuffle(arr) {
  for(let i=0 ; i<arr.length ; i++) {
    let rand = randInt(0, arr.length-1)
    swap(arr, i, rand)
  }
}

假如数组有n个元素，每次取值的范围都是从0到n-1，也就是都是n种可能性 总共的可能性数量就是n² 多数情况下它和n!都不相等，也不是其整数倍

验证概率相等

概率反映随机事件出现的可能性大小。随机事件是指在相同条件下，可能出现也可能不出现的事件。例如，从一批有正品和次品的商品中，随意抽取一件，“抽得的是正品”就是一个随机事件。设对某一随机现象进行了n次试验与观察，其中A事件出现了m次，即其出现的频率为m/n。经过大量反复试验，常有m/n越来越接近于某个确定的常数（此论断证明详见伯努利大数定律）。该常数即为事件A出现的概率

验证起来其实就是依照概率这个词的基本概念来的 运用尽可能多的样本来确定这个无限接近的常数

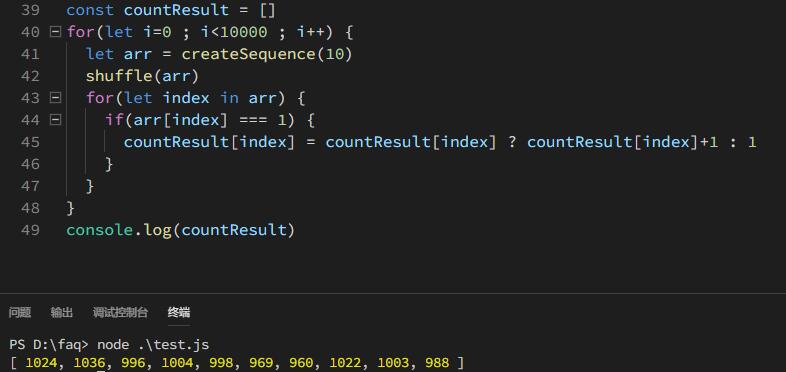
比如我们可以将上述的算法重复执行1万次，数字1出现在每个位置的次数应该比较接近 如果增大执行次数，1出现在每个位置的次数应该越来越接近相等

当然这样做创建大量对象，也是对内存的巨大消耗 其实我们也可以对同一个数组执行若干次乱序处理，如果每次乱序处理是完全随机的 那么每个数字出现在每个位置上的次数应该相对平均，实际的效果和上面的验证方式一致